To our knowledge, The Decision Modelbook[1] is the first publication to define a holistic approach to decision modeling that encompasses the formality of multiple forms of normalization through advanced normal forms. This is important because this is decision model science.
As a business analyst you are the all-important glue between the business and technology. Your skills range from various kinds of modeling to gathering of high-level as well as detailed robust requirements. Sometimes you operate in traditional systems development and sometimes within agile approaches. A business analyst’s responsibilities are wide and deep.
What Are the New Opportunities for Business Analysts?
Today, some of you already know that The Decision Model opens new opportunities for business analysts. That’s because The Decision Model is a business-friendly, technology-independent representation of business rules formalized as business logic. But there is more to know.
Our book and this month’s column resurrect the formal notion of normalization, giving it a new life in the emerging standard field of decision modeling. Specifically, we begin by exploring why normalization is important from a historical perspective. But more intriguing today is whether the notion of normalization is relevant (and important) to assets other than data. Specifically is it possible to apply the rigor of normalization to business logic in decision models? If so, what is its value and how do we define and apply it?
Historical Impact of Normalization
Normalization is a fancy word with an important history. Its importance lies in the fact that the Relational Model and its normal forms provided the database field with a stable, scientific foundation. The premise of this column is that a similar (but necessarily different) set of normal forms for The Decision Model should accomplish the same. And, for business analysts who often leaders the decision modeling, this is very good news indeed.
So, the remainder of this column reveals three decision model normal forms. It introduces their formal definitions and provides step-by-step illustrations using realistic examples[2].
Part 1: A Critical time for The Decision Model
But first, why introduce decision model normalization now? The reason is that decision modeling is well on its way to becoming the standard technique for representing, managing, and automating business logic of operational decisions, regulatory compliance, and best practices. Since publication of our book in 2009, various approaches and software for decision modeling are emerging and will continue to do so. And the OMG will be publishing a standard for Decision Modeling and Notation in 2013. As decision modeling comes of age, it is time to pose an important question - is decision modeling an art or is it partially based in rigor or science?
We believe that normalization is a cornerstone for true decision modeling. Without normalization, decision modelers can create useful diagrams, but these are not the same as delivering a more formal model. The Decision Model with normalization adds simple and practical rigor to the logic of business decisions in much the same way as the Relational Model did for data. So, let’s start by understanding the commonality between data and business logic, setting the stage for two normalizations.
Part 2: Seeking a Commonality between Data and Business Logic
It is important to point out that data and business logic are fundamentally different intellectual assets. Therefore, their normal forms cannot be identical. However, the similarities between the Relational Model and The Decision Model are interesting:
-
Each defines a technology-independent way of organizing an important, somewhat intangible asset
-
Each is implementable in various technologies
-
Each is a solution to an unsolved problem of its day.
With these points in mind, we can base their normal forms on the specific purpose of each normal form. This means recognizing that each normal form results in a structure delivering the full value of that normal form by design. In this way, the purpose of each normal form is universal across The Decision Model, the Relational Model, and any other usage that may emerge in the future.
Part 3: Where Normalization Begins and Why
First Normal Form is where it all begins. In fact, First Normal Form is required for data to be sound from a relational model perspective. First Normal Form is also required for business logic to be sound from The Decision Model perspective.
First Normal Form is required for one and only one reason, It delivers a simple single representation for an entire model of data or of business logic. The important point is that the entire content of a model in First Normal Form is represented in one and only one way leading to one and only one set of governing principles. So, every structure in The Decision Model looks and feels the same as every other structure. Likewise, every structure in Relational Model looks and feels the same as every other structure. This is goodness.
For example, a relational model never contains hierarchical, networked, or indexed data structures that are visible to non-technical users. By design, it presents to non-technical users only relations adhering to First Normal Form.
Likewise, The Decision Model never contains variations of decision trees, decision tables, or other types of logical structures that are visible to non-technical users. Instead, it presents to non-technical users only Rule Families adhering to First Normal Form.
Part 4: A Refresher on the Normalization Process
While First Normal Form is mandatory, all other normal forms are optional, but desirable. The process of normalization starts with a structure in First Normal Form and simply decomposes it to deliver the highest integrity of data or of business logic. Highest integrity is reached when it is possible to make additions, deletions, and updates in one place and have these propagate throughout the model using pre-defined naturally occurring relationships. That’s because the entire model is a holistic deliverable, operating according to pre-defined principles as one integrated unit. In this way, the model is free of anomalies (i.e., errors) that can arise from insert, update, and delete activities.
Each higher level of normalization usually results in the decomposition of an original structure into multiple ones of higher quality. Any argument against more versus fewer structures theoretically makes no sense. What makes sense is choosing between higher and lower quality. That is what is at stake.
This ultimate simplicity of First Normal Form delivers business-friendly, rigorous, and easily maintained models. Let’s explore the first three normal forms for The Decision Model, one at a time, in detail.
Part 5: First Normal Form
As indicated above, the universal purpose of First Normal Form (for data and business logic) is to produce a model is represented and interpreted in one and only one way.
First Normal Form for data and business logic applies to the population of a structure already adhering to special properties. Specifically, such a structure has the following special properties to start with:
-
Is two-dimensional,
-
Entries in columns are of the same kind,
-
No duplicate rows; each row is unique,
-
Each column has a unique name,
-
Sequence of columns and sequence of rows is insignificant.
However, the differences in normal forms between data and business logic start with First Normal Form. First Normal Form for data applies to a collection of individual attributes that together convey information. On the other hand, First Normal Form for business logic applies to a collection of logical expressions that together infer a conclusion.
First Normal Form in The Decision Model (TDM)
When a business logic structure with the above properties is translated into First Normal Form, the result is a business logic record that, in every row there is one and only one conclusion column (TDM Principle 5), at each row-and-column position there is always an atomic logical expression[3] conforming to the heading (TDM principle 3), and all populated condition cells evaluate to true for the corresponding conclusion cell to be true (TDM principle 6).
Most people explain decision model First Normal Form as a set of rows in a Rule Family in which conditions are connected only by AND meaning there are no ORs, BUTs, ELSEs, YET, or OTHERWISEs.
Step by Step First Normal Form in The Decision Model
In the real world, there are a lot of business lookup tables. These come in all kinds of shapes and formats. The act of transforming a business lookup table into First Normal Form means recasting it in the one and only one way so that everyone knows how to interpret it. Figure 1is a real-world business lookup table[4] as our starting point.
| Mortgage Purpose Type and Property Type |
Max LTV w/o Secondary Financing |
Max LTV w Secondary Financing |
| 1-unit primary residence |
95% |
95% |
| 2-4 unit primary residence |
80% |
75% |
| Second home |
85% |
80% |
Figure 1: Typical Business Lookup Table
The transformation to decision model First Normal Form has three steps. The first step is to identify the Rule Family’s single conclusion column heading (Remember: TDM Principle 5). After studying the business lookup table in Figure 1to understand how to read it, we can conclude that it provides the means for finding the Max LTV[5] for various mortgage purposes, property types, and secondary financing. So, the Rule Family’s conclusion values are the percentages inside the cells of the second two columns.
The second step is to identify the Rule Family’s atomic condition column headings (Remember TDM Principle 3). Searching for conditions in Figure 1, we find that its first column heading contains two conditions (i.e., so it is an overloaded data field). These two conditions are Mortgage Purpose Type and Property Type. Further study reveals there is another condition hidden in the column heading of the second two columns. This condition is Secondary Financing.
The third step is to fill in the rows with populated condition cells leading to the corresponding populated conclusion cell constrained by using only ANDs between them (Remember TDM Principles 3 and 6). The resulting Rule Family (in First Normal Form) is in Figure 2.
| Row ID |
Rule Pattern |
Conditions |
Conclusion |
| Mortgage Purpose |
Property Type |
Secondary Financing |
Max LTV |
| 1 |
1 |
Is |
Primary residence |
Is |
1-unit |
Is |
No |
Is |
95% |
| 2 |
1 |
Is |
Primary residence |
Is |
1-unit |
Is |
Yes |
Is |
95% |
| 3 |
2 |
Is |
Primary residence |
Is In |
{2-unit, 3-unit, 4-unit} |
Is |
No |
Is |
80% |
| 4 |
2 |
Is |
Primary residence |
Is In |
{2-unit, 3-unit, 4-unit} |
Is |
Yes |
Is |
75% |
| 5 |
3 |
Is |
Second home |
|
|
Is |
No |
Is |
85% |
| 6 |
3 |
Is |
Second home |
|
|
Is |
Yes |
Is |
80% |
Figure 2: First Normal Form
Hopefully, you appreciate the clarity of Figure 2. Each column heading and its content are in atomic (i.e., non-decomposable) form. All populated condition cells lead to or infer the corresponding conclusion column cell. A subtle but important realization is that, because the populated condition cells lead to the corresponding conclusion cells, the conclusion column is functionally dependent on its concatenated populated condition columns. Functional dependency is an important ingredient in defining other normal forms. Also valuable is that every Rule Family in decision models have the same look and feel as the one in Figure 2.
So, these two properties: standard look and feel and functional dependency, set the stage for new, similar forms of normalization.
Part 6: Second Normal Form
The universal purpose of Second Normal Form (for data and business logic) is to eliminate functional dependencies involving only part of the identifier. That is, there must be no partial key dependencies.
Second Normal Form in The Decision Model
Second Normal Form in The Decision Model means business logic is already in First Normal Form and also every conclusion value is fully functionally dependent (i.e., inferentially dependent) on the entire set of populated condition columns. More simply, there is no populated condition cell that is irrelevant to deciding the corresponding populated conclusion cell.
Second Normal Form is easier to understand through an example than through its definition.
Step by Step Second Normal in The Decision Model
A careful look at Figure 2 reveals that it is not in Second Normal Form. That’s because Secondary Financing for Mortgage Purpose Type of “Primary residence” and Property Type of “1-unit”is irrelevant to the conclusion value. This is obvious because the value for Max LTV is “95%”for this Mortgage Purpose Type and Property Type regardless of the value of Secondary Financing. So, Secondary Financing is an unnecessary condition.
Unnecessary conditions are bad. They add unnecessary redundancy, which correlates to unnecessary complexity, and the undesirable likelihood of introducing errors during updates. Maintaining values for these rows for Secondary Financing is useless and error-prone, and these values have no effect on the conclusion. Removing the contents of those cells leaves two identical rows (Row ID 1 and 2) as shown in Figure 3.
| Row ID |
Rule Pattern |
Conditions |
Conclusion |
| Mortgage Purpose |
Property Type |
Secondary Financing |
|
|
| 1 |
1 |
Is |
Primary residence |
Is |
1-unit |
|
|
Is |
95% |
| 2 |
1 |
Is |
Primary residence |
Is |
1-unit |
|
|
Is |
95% |
| 3 |
2 |
Is |
Primary residence |
Is In |
{2-unit, 3-unit, 4-unit} |
Is |
No |
Is |
80% |
| 4 |
2 |
Is |
Primary residence |
Is In |
{2-unit, 3-unit, 4-unit} |
Is |
Yes |
Is |
75% |
| 5 |
3 |
Is |
Second home |
|
|
Is |
No |
Is |
85% |
| 6 |
3 |
Is |
Second home |
|
|
Is |
Yes |
Is |
80% |
Figure 3: Removing Irrelevant Condition Cells
Studying Figure 3, it is easy to see that it is not now even in First Normal Form. That’s because it contains duplicate rows (Row ID 1 and 2) which violates one of the starting properties.
Duplicate rows are bad. They are another example of unnecessary redundancy and its associated problems. Deleting one of these rows results in the Rule Family in Figure 4.
| Row ID |
Rule Pattern |
Conditions |
Conclusion |
| Mortgage Purpose |
Property Type |
Secondary Financing |
|
|
| 1 |
1 |
Is |
Primary residence |
Is |
1-unit |
|
|
Is |
95% |
| 2 |
2 |
Is |
Primary residence |
Is In |
{2-unit, 3-unit, 4-unit} |
Is |
No |
Is |
80% |
| 3 |
2 |
Is |
Primary residence |
Is In |
{2-unit, 3-unit, 4-unit} |
Is |
Yes |
Is |
75% |
| 4 |
3 |
Is |
Second home |
|
|
Is |
No |
Is |
85% |
| 5 |
3 |
Is |
Second home |
|
|
Is |
Yes |
Is |
80% |
Figure 4: Second Normal Form
Part 7: Third Normal Form
The universal purpose of Third Normal Form (for data and business logic) is to decompose Second Normal Form structures to eliminate transitive dependencies in which non-key portions depend on other non-key portions.
Third Normal Form for Business Logic
Third Normal Form in The Decision Model means business logic is already in Second First Normal Form and also every populated condition is non- transitively functionality dependent (i.e, inferentially dependent) on other conditions. Simply stated, there is no condition column that actually represents a conclusion related to other condition columns.
Third Normal Form is easier to understand through an example than through its definition.
Third Normal Form Example for The Decision Model
Since the Rule Family in Figure 4 is already in Third Normal Form, let’s consider a different Rule Family, the one in Figure 5. This is a fictitious but realistic table of logic for determining if a certain type of property and mortgage qualify for a homeowner’s relief program.
| Row ID |
Rule Pattern |
Conditions |
Conclusion |
| Property Unit Quantity |
Mortgage Unpaid Balance Amount |
Mortgage Unpaid Balance Amount Eligibility |
Mortgage Origination Date |
Homeowner Mortgage Relief Program Eligibility |
| 1 |
1 |
Is |
1 |
Is Less Than |
$700k |
Is |
Eligible |
Is On or Before the Date |
1/1/2013 |
Is |
Eligible |
| 2 |
1 |
Is |
2 |
Is Less Than |
$900k |
Is |
Eligible |
Is On or Before the Date |
1/1/2013 |
Is |
Eligible |
| 3 |
1 |
Is |
3 |
Is Less Than |
$1000k |
Is |
Eligible |
Is On or Before the Date |
1/1/2013 |
Is |
Eligible |
| 4 |
1 |
Is |
4 |
Is Less Than |
$1400k |
Is |
Eligible |
Is On or Before the Date |
1/1/2013 |
Is |
Eligible |
| 5 |
2 |
Is |
1 |
Is Greater Than or Equal To |
$700k |
Is |
Not Eligible |
|
|
Is |
Not Eligible |
| 6 |
2 |
Is |
2 |
Is Greater Than or Equal To |
$900k |
Is |
Not Eligible |
|
|
Is |
Not Eligible |
| 7 |
2 |
Is |
3 |
Is Greater Than or Equal To |
$1000k |
Is |
Not Eligible |
|
|
Is |
Not Eligible |
| 8 |
2 |
Is |
4 |
Is Greater Than or Equal To |
$1400k |
Is |
Not Eligible |
|
|
Is |
Not Eligible |
| 9 |
|
|
|
|
|
|
|
Is After the Date |
1/1/2013 |
is |
Not Eligible |
Figure 5: Not in Third Normal Form
Looking closely, the conditions for Property Unit Quantity and Mortgage Unpaid Balance Amount appear to determine the value in the condition column Mortgage Unpaid Balance Amount Eligibility. Specifically, Row IDs 1-4 seem to correlate to an “Eligible” value in the condition column for Mortgage Unpaid Balance Amount Eligibility while Row IDs 5-8 appear to correlate to a “Not Eligible” for the condition Mortgage Unpaid Balance Amount Eligibility. Moreover, when the value of Mortgage Unpaid Balance Amount Eligibility is “Eligible”, the value in the conclusion column is “Eligible.” When the value of Unpaid Balance Amount Eligibility is “Not Eligible”, the value in the conclusion column is “Not Eligible.” If business experts validate this finding, it represents a transitive dependency among condition columns.
As you might have guessed by now, transitive dependencies are bad. Transitive dependencies are yet another example of unnecessary redundancy and its associated problems.
Eliminating this transitive dependency means moving the first three condition columns to their own Rule Family whose conclusion is Mortgage Unpaid Balance Amount Eligibility. The original Rule Family retains Mortgage Unpaid Balance Amount Eligibility as a condition along with Mortgage Origination Date. The resulting Rule Families are in Figure 6.
| Row ID |
Rule Pattern |
Conditions |
Conclusion |
| Mortgage Unpaid Balance Amount Eligibility |
Mortgage Origination Date |
Homeowner Mortgage Relief Program Eligibility |
| 1 |
1 |
Is |
Eligible |
Is On or Before the Date |
1/1/2013 |
Is |
Eligible |
| 2 |
2 |
Is |
Not Eligible |
|
|
Is |
Not Eligible |
| 3 |
3 |
|
|
Is After the Date |
1/1/2013 |
Is |
Not Eligible |
| Row ID |
Rule Pattern |
Conditions |
Conclusion |
| Property Unit Quantity |
Mortgage Unpaid Balance Amount |
Mortgage Unpaid Balance Amount Eligibility |
| 1 |
1 |
Is |
1 |
Is Less Than |
$700k |
Is |
Eligible |
| 2 |
1 |
Is |
2 |
Is Less Than |
$900k |
Is |
Eligible |
| 3 |
1 |
Is |
3 |
Is Less Than |
$1000k |
Is |
Eligible |
| 4 |
1 |
Is |
4 |
Is Less Than |
$1400k |
Is |
Eligible |
| 5 |
1 |
Is |
1 |
Is Greater Than or Equal To |
$700k |
Is |
Not Eligible |
| 6 |
1 |
Is |
2 |
Is Greater Than or Equal To |
$900k |
Is |
Not Eligible |
| 7 |
1 |
Is |
3 |
Is Greater Than or Equal To |
$1000k |
Is |
Not Eligible |
| 8 |
1 |
Is |
4 |
Is Greater Than or Equal To |
$1400k |
Is |
Not Eligible |
Figure 6: Third Normal Form
Notice what has happened. When transformed to Third Normal Form, the original First Normal Form structure became two Rule Families with an inferential relationship between them. The resulting two Rule Families also contain the fewest quantity of rows needed to represent the full logic. Interpretation and future updates become simpler.
Part 8: A Word about Higher Normal Forms
Originally, in 2009, we stated “The Decision Model is introduced in this book with three basic normal forms (first, second, and third). Higher normal forms are likely to exist. The higher the normal form, the more desirable the Decision Model structure and content.” As of 2013, we have discovered fourth and fifth normal forms in decision models. This is not a surprise. It underscores the value of The Decision Model and its science.
Part 9: Why this is Good News for Business Analysts Professionals
Imagine the value of normalization in delivering large, complex decision models where the entire model is in Third Normal Form or higher, such as the one in Figure 7. This means the entire model is of highest integrity with the minimal representation (i.e., least unnecessary redundancy) and is compliant with all corresponding integrity principles. This is when the useful diagram becomes a living formal model – a new business asset.
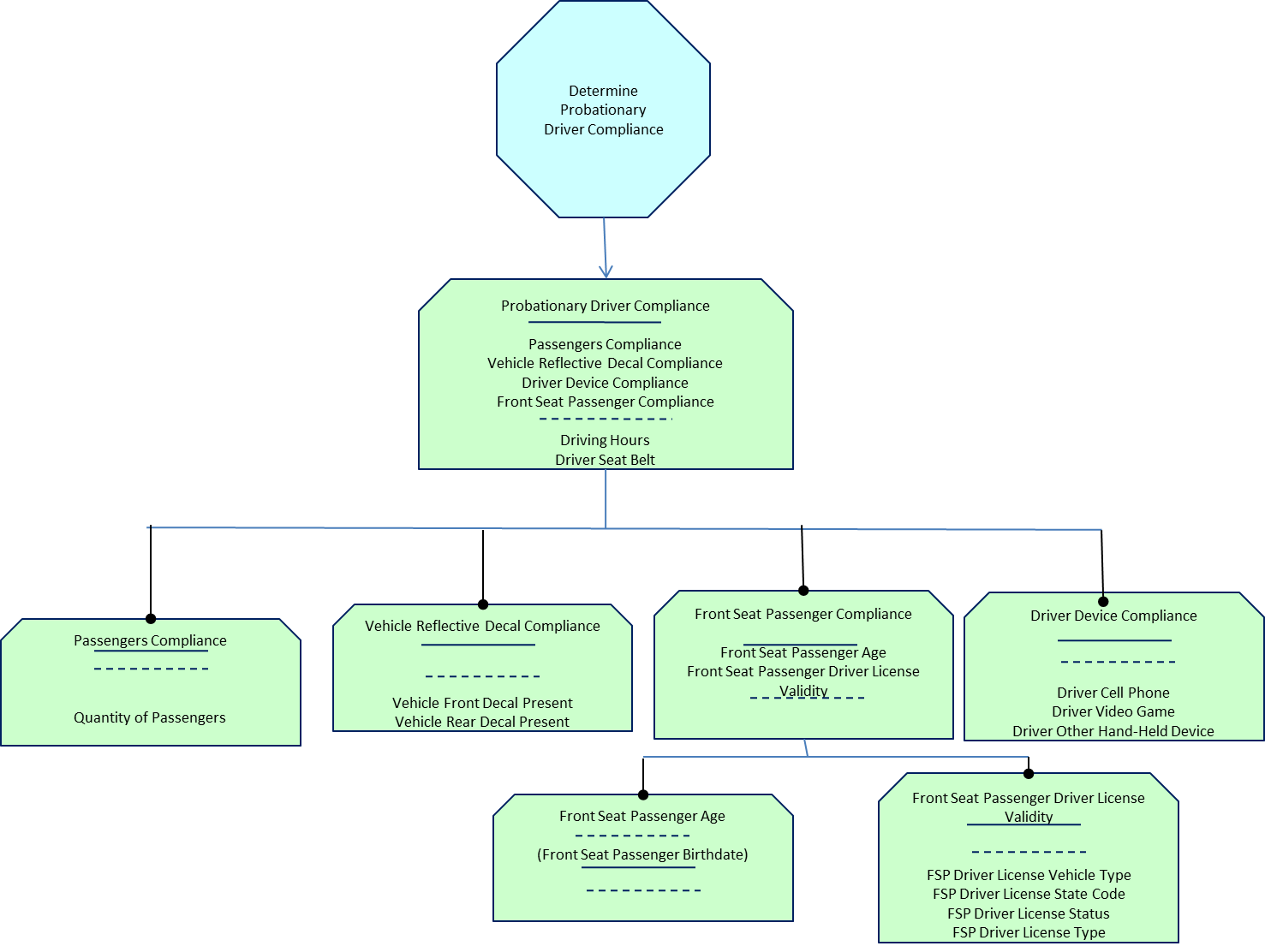
Figure 7: Real-World Decision Model all in Third Normal Form or Higher
(higher resolution version)
Decision Modeling is a recognized practice in companies of all sizes and in all industries. Examples of new roles appropriate for business analysts with respect to decision models are:
-
Decision modeler who translates business input into normalized Rule Families connected together in decision models
-
Decision model reviewer who seeks and fixes logic and normalization errors
-
Glossary administrator who refines condition and conclusion headings with fact type business-friendly names, definitions, and domains.
Interesting Points to Remember
Below are the most important points to remember about decision model normalization.
-
Never be afraid to normalize decision models because higher normal forms deliver higher quality logic.
-
First Normal Form is the most important and often the least understood. It dictates a universal structure from which higher forms of normalization are possible.
-
Don’t be concerned if normalization delivers more structures in your decision models than expected. The goal is to achieve highest integrity. In fact, if the history of data normalization is proof, the more structures the better.
-
Don’t feel compelled to memorize the normal forms. Simply follow your intuition regarding structures that feel right and those that feel wrong. As always, if you find unnecessary redundancy, do what comes quite naturally - decompose!
Most important of all, be sure your decision modeling approach includes the science of normalization. Otherwise, you are missing the most important part of decision modeling and its greatest value[6].
Authors: Barbara von Halle and Larry Goldberg of Knowledge Partners International, LLC (KPI)
 Larry Goldberg is Managing Partner of Knowledge Partners International, LLC (KPI), has over thirty years of experience in building technology based companies on three continents, and in which the focus was rules-based technologies and applications. Commercial applications in which he played a primary architectural role include such diverse domains as healthcare, supply chain, and property & casualty insurance.
Larry Goldberg is Managing Partner of Knowledge Partners International, LLC (KPI), has over thirty years of experience in building technology based companies on three continents, and in which the focus was rules-based technologies and applications. Commercial applications in which he played a primary architectural role include such diverse domains as healthcare, supply chain, and property & casualty insurance.
 Barbara von Halle is Managing Partner of Knowledge Partners International, LLC (KPI). She is co-inventor of the Decision Model and co-author of The Decision Model: A Business Logic Framework Linking Business and Technology published by Auerbach Publications/Taylor and Francis LLC 2009.
Barbara von Halle is Managing Partner of Knowledge Partners International, LLC (KPI). She is co-inventor of the Decision Model and co-author of The Decision Model: A Business Logic Framework Linking Business and Technology published by Auerbach Publications/Taylor and Francis LLC 2009.
Larry and Barb can be found at www.TheDecisionModel.com.
[1] von Halle, Barbara and Larry Goldberg, The Decision Model: A Business Logic Framework Linking Business and Technology, © 2009 Auerbach Publications/Taylor & Francis, LLC.
[2]Readers interested in examples of data normal forms, see Chapter 11.
[3] An atomic logical expression in The Decision Model is of the form “operator + operand”
[4] This is a partial representation of the LTV/TLTV/HTLTV Ratio Requirements for Conforming Mortgages published at http://www.freddiemac.com/sell/factsheets/ltv_tltv.htm
[5] Maximum loan-to-value ratio
[6] Readers interested in a more in-depth analysis of the Relational Model and The Decision Model will find one in Chapter 11.